Minimization

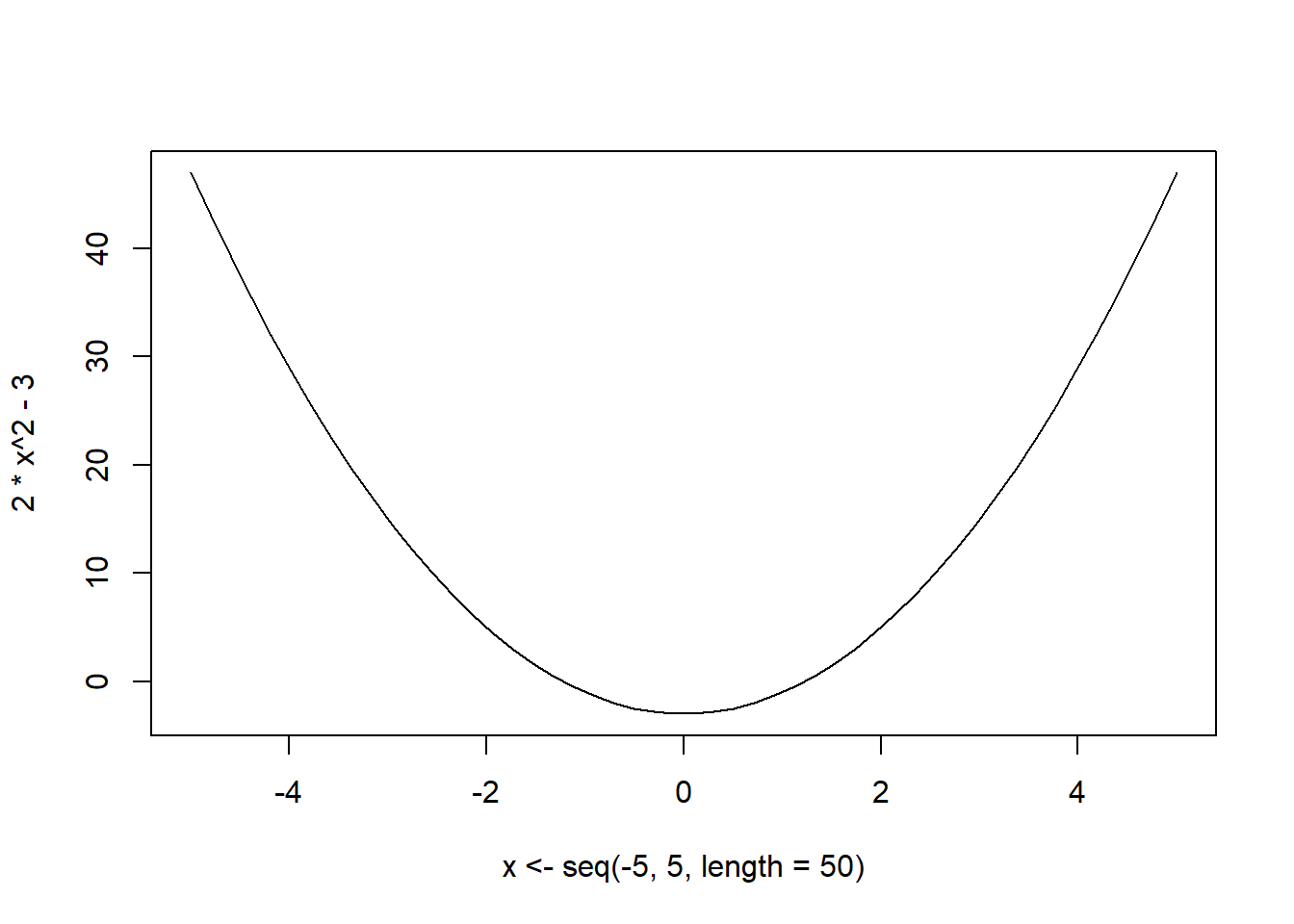
Previously we looked at root finding methods. Suppose instead of obtaining the root, we want to obtain the optimal point of the function. ie either maximum or minimum. We know that at the optimum, the gradient is 0. Thus for optimization, we opt to obtain the root of the gradient ie \(f'(x) = 0\).

To do this, we use the methods described above but we use \(f'(x)\) as our function of interest.

Therefore the updating methodology becomes:

\[ x_{n+1} = x_n \pm \alpha f'(x) \]

This is called the GRADIENT/STEEPEST DESCENT(ASCENT) ALGORITHM.

ie if we use addition the we talk of ascent and if we use subtraction we talk of descent.

The choice of \(\alpha\) corresponds to the different methods available.

Newton Raphson:

For this method \(\alpha = \frac{1}{f''(x)}\) . If \(f\) is multivariate, then we have \(\alpha = H^{-1}(x)\) where \(H(x) = \nabla^2f(x) = \frac{\partial^2 f(x)}{\partial x \partial x^\top}\) ie 2nd order derivative of the function evaluated at \(x\)

Examples:

  1. Find the minimum of \(f(x) = 2x^2 - 3\)

    First we can plot to see how the function looks like

    plot(x <- seq(-5,5,length = 50), 2 * x**2 - 3, ty='l')

    import matplotlib.pyplot as plt, numpy as np
plt.clf()
plt.plot(x := np.linspace(-5,5), 2 * x**2 - 3)
plt.show()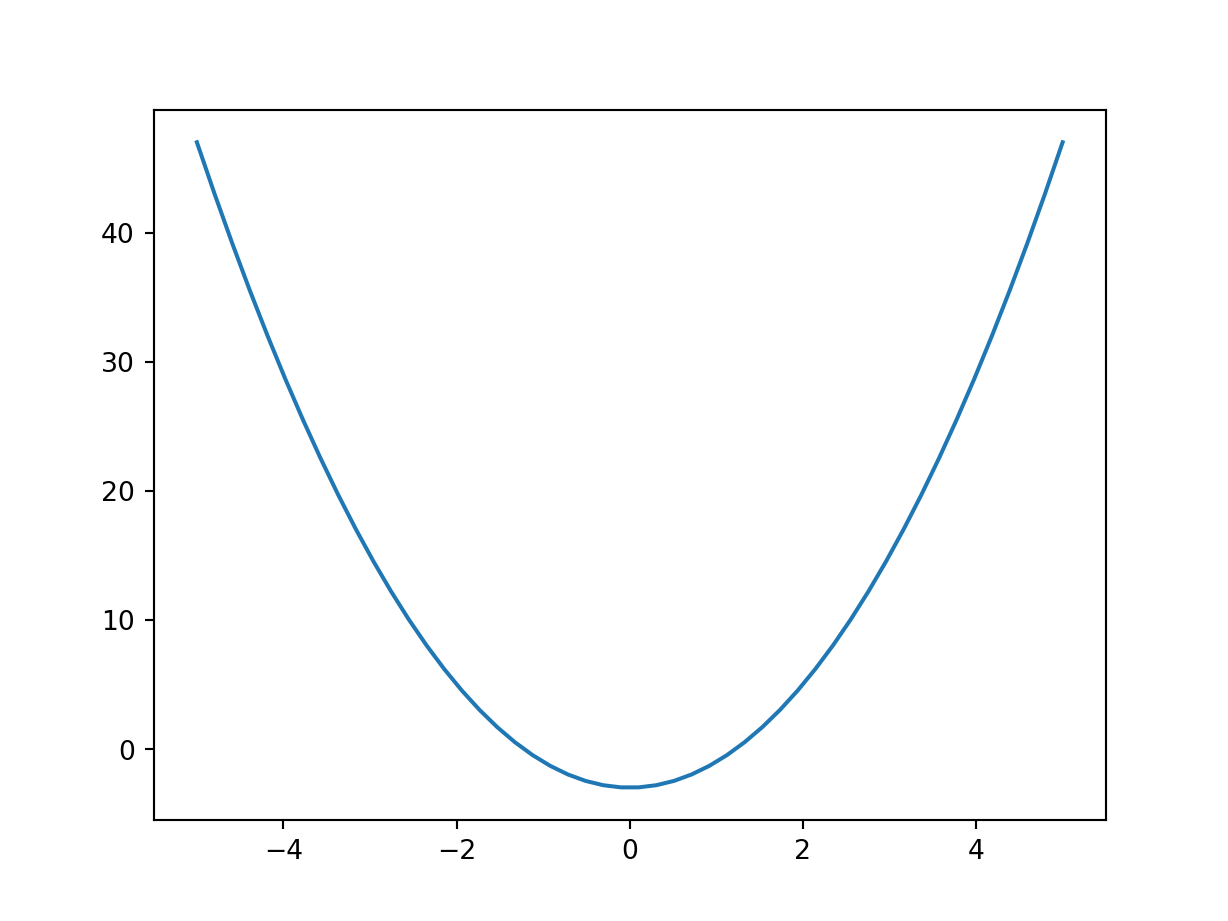

    We can see that the optimum/minimum occurs at \(x=0\). Now we can solve this analytically:

\[ f'(x) = 4x \therefore f'(x) = 0 \implies x=0\\ f''(0) = 4 > 0 \implies x=0 \text{ is a minimum} \]

optimize(\(x)2*x**2 -3, c(-100,100))
$minimum
[1] -3.552714e-15

$objective
[1] -3
from scipy.optimize import minimize_scalar
minimize_scalar(lambda x: 2*x**2 - 3, [-100,100])
 message: 
          Optimization terminated successfully;
          The returned value satisfies the termination criteria
          (using xtol = 1.48e-08 )
 success: True
     fun: -3.0
       x: -3.78263270776151e-11
     nit: 43
    nfev: 46

Notice that since the 2nd derivative is constant, using the newton raphson, only one iteration is enough.

x <- -100
x <- x - 4*x/4
x
[1] 0
x = -100
x -= 4*x/4
x
0.0

Find the maximum of the following function.

\[ \begin{array}{rl} f(x,y) =2xy+2x-x^2 - 2y^2 &\quad\quad 0<x<4\\ &\quad\quad0.5<y<2.5 \end{array} \]

Solution:

\[ f'(x,y) = \begin{pmatrix}2y + 2 - 2x\\2x - 4y\end{pmatrix}\\ H = \begin{bmatrix}\frac{\partial^2 f}{\partial x^2}&\frac{\partial^2 f}{\partial x\partial y}\\\frac{\partial^2 f}{\partial y\partial x}&\frac{\partial^2f}{\partial y^2}\end{bmatrix} = \begin{bmatrix}-2&2\\2&-4\end{bmatrix}\\ H^{-1} = \frac{1}{4}\begin{bmatrix}-4&-2\\-2&-2\end{bmatrix} = -\frac{1}{2}\begin{bmatrix}2&1\\1&1\end{bmatrix} \]

f <- function(x){
    2*x[1]*x[2] + 2*x[1] - x[1]^2 - 2*x[2]^2
}

fprime <- function(x) c(2*x[2]+2-2*x[1], 2*x[1]-4*x[2])

alpha <- -0.5*matrix(c(2,1,1,1),2)
x <- c(-100,-100)
x <- x - alpha%*%fprime(x) #matrix multiplication
x
     [,1]
[1,]    2
[2,]    1
f(x)
[1] 2
fprime(x)
[1] 0 0
import numpy as np

def f(x):
    return 2*x[0]*x[1] + 2*x[0] - x[0]**2 - 2*x[1]**2
  
def fprime(x):
  return np.r_[2*x[1] + 2 - 2*x[0], 2*x[0]-4*x[1]]
  
alpha = -0.5 * np.array([[2,1],[1,1]])
x = np.r_[-100.0,-100]

x -= alpha @ fprime(x) #matrix multiplication
x
array([2., 1.])
f(x)
2.0
fprime(x)
array([0., 0.])

Notice how we only did one evaluation and we obtained the results. How is this possible? That is because the second derivative is free of the parameters, thus we directly converge to the solution. Of course in your implementation, you should make use of loops.

In the example above, the minimum occurs at the point \((2,1)\) with the minimum value of \(2\)

We could easily use the optim function in R to do the same: Note that the function does minimization by default. To do maximization, we negate the function.

optim(c(-100,-100), \(x) -f(x))
$par
[1] 2.0028621 0.9999563

$value
[1] -1.999992

$counts
function gradient 
      69       NA 

$convergence
[1] 0

$message
NULL

Note that we could also use used fnscale = -1 to indicate that we are doing maximization rather than minimization

optim(c(-100,-100), f, control = list(fnscale = -1))
$par
[1] 2.0028621 0.9999563

$value
[1] 1.999992

$counts
function gradient 
      69       NA 

$convergence
[1] 0

$message
NULL

We could easily use the minimize function in python to do the same: Note that the function does minimization by default. To do maximization, we negate the function.

from scipy.optimize import minimize
minimize(lambda x: -f(x), (-100,-100))
  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: -1.9999999999948197
        x: [ 2.000e+00  1.000e+00]
      nit: 4
      jac: [ 4.411e-06 -5.543e-06]
 hess_inv: [[ 1.001e+00  4.998e-01]
            [ 4.998e-01  5.001e-01]]
     nfev: 21
     njev: 7

Root finding as a minimization Problem

Sometimes the problem of root finding can be structured as an optimization problem and then optim or optimize functions could be used.

For example given that

\[ \mu = \frac{\alpha}{\beta} \text{ and } \sigma^2 = \frac{\alpha}{\beta^2} \]

and also that \(\mu=5, \sigma^2=10\) solve for \(\alpha, \beta\)

How do we go about this?

We can first combine two into one. ie \(\frac{\alpha}{\beta} - \frac{\alpha}{\beta^2}=-5\) This becomes a root finding problem ie solve for \((\alpha, \beta)\) such that \(f(\alpha,\beta)=0\) . Note that we can transform this into a minimization problem. ie we do not want to go below \(0\). we are interested in a values of \((\alpha,\beta)\) such that the minimum \(f\) is \(0\). Thus we can rewrite \(f\) as:

  1. \(f(\alpha, \beta) = \left|\frac{\alpha}{\beta} - 5\right|+\left|\frac{\alpha}{\beta^2} - 10\right|\)

  2. \(f(\alpha, \beta) = \left(\frac{\alpha}{\beta} - 5\right)^2 + \left( \frac{\alpha}{\beta^2} -10\right)^2\)

The two functions in this case would yield the same results since \(f(\alpha, \beta)\ge0\)

Using absolute

optim(c(1,1), \(par)abs(par[1]/par[2]^2-10) + abs(par[1]/par[2] - 5))
$par
[1] 2.5 0.5

$value
[1] 4.070251e-07

$counts
function gradient 
     135       NA 

$convergence
[1] 0

$message
NULL

Using square

optim(c(1,1), \(par)(par[1]/par[2]^2-10)^2 + (par[1]/par[2] - 5)^2)
$par
[1] 2.4994315 0.4999561

$value
[1] 7.557839e-07

$counts
function gradient 
      73       NA 

$convergence
[1] 0

$message
NULL

Using square

from scipy.optimize import minimize
minimize(lambda par:(par[0]/par[1]**2-10)**2 + (par[0]/par[1] - 5)**2,(1,1))
  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: 2.562549482808408e-12
        x: [ 2.500e+00  5.000e-01]
      nit: 11
      jac: [ 8.672e-07 -8.404e-06]
 hess_inv: [[ 5.309e-01  5.615e-02]
            [ 5.615e-02  6.219e-03]]
     nfev: 63
     njev: 21

From the above, we obtain \(\alpha = 2.5, \beta=0.5\). Notice that although the original problem did not involve minimization, we structured it in a way that allowed us to do minimization.

Recall the function \(f(x) = \log(x) - e^{-x}\), we could do the same to this in order to use the optim or optimize function:

Our goal is to get \(x\) such that \(f(x) = 0\). We could restructure our function such that we square or take absolute \(\mathcal{L} = \left(\log(x) - e^{-x}\right)^2\)

optimize(\(x)(log(x)-exp(-x))^2, lower = 0, upper = 100)
$minimum
[1] 1.309787

$objective
[1] 1.676184e-10
from scipy.optimize import minimize_scalar
import numpy as np

minimize_scalar(lambda x:(np.log(x)-np.exp(-x))**2,[0,100])
 message: 
          Optimization terminated successfully;
          The returned value satisfies the termination criteria
          (using xtol = 1.48e-08 )
 success: True
     fun: 2.6200587055821345e-18
       x: 1.3097995873705703
     nit: 20
    nfev: 23

<string>:2: RuntimeWarning: divide by zero encountered in log

For example if we wanted to solve for \(x\) in \(x^2 e^{3x} +x\log(x) = 10\)

optimise(\(x)(x^2*exp(3*x)+x*log(x) - 10)^2, c(0, 100))
$minimum
[1] 0.866875

$objective
[1] 1.182101e-08

minimize_scalar(lambda x: (x**2*np.exp(3*x)+x*np.log(x) - 10)**2, (0, 100))

from scipy.optimize import minimize_scalar
import numpy as np

minimize_scalar(lambda x:(x**2*np.exp(3*x)+x*np.log(x) - 10)**2, (0, 100))
 message: The algorithm terminated without finding a valid bracket. Consider trying different initial points.
 success: False
     fun: nan
       x: nan
     nit: 0
    nfev: 3

<string>:2: RuntimeWarning: invalid value encountered in scalar multiply
<string>:2: RuntimeWarning: overflow encountered in exp

To remove the warning, we redefine our function. We know that log only works in positive values, therefore we bound the domain by using method='bounded':

minimize_scalar(lambda x: (x**2*np.exp(3*x)+x*np.log(x) - 10)**2, bounds=(0, 100), method='bounded')
 message: Solution found.
 success: True
  status: 0
     fun: 6.172707419354954e-09
       x: 0.8668715632395412
     nit: 61
    nfev: 61

At the same time, as we are interested in minimization, we could let the function return a huge number whenever x is outside of the domain. Thus constraining the optimization to only occur within the feasible region.

def f(x):
  if x<=0:
    return 1e10 # A very big number
  else:
    return (x**2*np.exp(3*x)+x*np.log(x) - 10)**2
  
minimize_scalar(f , (1e-20, 100))
 message: 
          Optimization terminated successfully;
          The returned value satisfies the termination criteria
          (using xtol = 1.48e-08 )
 success: True
     fun: 9.45467744810933e-15
       x: 0.866873000785157
     nit: 23
    nfev: 26

Note that in the above, we have to specify the interval in which we perceive the solution to lie in. What if we did not know this? we could use optim function in R or mimimize function in Python.

optim(1, \(x)(x^2*exp(3*x)+x*log(x) - 10)^2)
Warning in optim(1, function(x) (x^2 * exp(3 * x) + x * log(x) - 10)^2): one-dimensional optimization by Nelder-Mead is unreliable:
use "Brent" or optimize() directly
$par
[1] 0.8668945

$value
[1] 1.381145e-06

$counts
function gradient 
      26       NA 

$convergence
[1] 0

$message
NULL
minimize(lambda x: (x**2*np.exp(3*x) + x*np.log(x) - 10)**2, 2)
  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: 1.1384534173688652e-13
        x: [ 8.669e-01]
      nit: 10
      jac: [ 7.564e-06]
 hess_inv: [[ 1.677e-04]]
     nfev: 28
     njev: 14

Note that function throws a warning regarding the method used. You can learn about the different methods provided in R/python.

Similarly we could have directly solved the problem using uniroot in R or root in Python since this is a root finding problem.

uniroot(\(x)x^2*exp(3*x) + x*log(x)-10, interval = c(1e-4, 100))
$root
[1] 0.8668723

$f.root
[1] -3.96713e-05

$iter
[1] 20

$init.it
[1] NA

$estim.prec
[1] 6.747708e-05
from scipy.optimize import root_scalar
root_scalar(lambda x: x**2*np.exp(3*x) + x*np.log(x)-10, bracket = (1e-4, 100))
      converged: True
           flag: converged
 function_calls: 23
     iterations: 22
           root: 0.8668730025669631

Why are we learning about transforming root finding problem as a optimization problem? That is because the methods provided in most languages are for optimization rather than root finding. Note that the uniroot function for example can only find roots for a univariate function. No methods have been provided for multivariate functions. We thus have to be skillful on converting the root finding problems to optimization problems. Mostly just rewrite the equation and square it. On the other hand Python provides the root function which can be used for multivariate problems

ie to find the root of \(f(x) = c\) is similar to minimizing \(g(x) = \left(f(x) - c\right)^2\) . We aim at minimizing the square of the difference between the value \(c\) and the value of the function evaluated at \(x\). This difference is called the error. ie \(\epsilon = c - f(x)\) . If the error is 0, then the value of \(x\) that gives us this 0 error is the same value of \(x\) that gives us \(c\) when the function is evaluated at it.

In case we have a multivariate function, we sum all the squared error terms. ie

\[ \sum_{i}\epsilon^2 = \sum_{i}\left(c_i - f(x_i)\right)^2 \]

This is the formula we used when solving for \(\alpha\) and \(\beta\) above. We note that we had two terms and each term had to be equal to something. ie the first term had to be equal to 5 and the second term had to be equal to 10. So we summed the square of the errors of each and minimized that.

Note that we could take the absolute value of each error term. But the absolute value is not differentiable everywhere, and neither is is smooth. We therefore will stick to using the squared errors.

Quiz: What happens when we do not take absolute values/square the difference? Why is that the case?

Lets look at another example:

Suppose we had 2 points ie \((1,2),\quad(2,3)\) we can write the equation of a line:

\[ m = \frac{3-2}{2-1} = 1\implies y = x + 1 \]

Could we find this equation using optimization? The equation of a line is given as \(y = mx +b\)

We would write the problem as:

\[ \begin{pmatrix}2\\3\end{pmatrix}= \begin{pmatrix}1\\2\end{pmatrix}m + \begin{pmatrix}1\\1\end{pmatrix}b \]

Now This is a simultaneous equation that you had solved before:

fn <- function(p){
  m <- p[1]
  b <- p[2]
  (1*m + 1*b - 2)^2 + (2*m + 1*b - 3)^2
}
start <- c(m = 0, b = 0)
optim(start, fn, method = 'BFGS')
$par
m b 
1 1 

$value
[1] 1.93566e-19

$counts
function gradient 
      14        8 

$convergence
[1] 0

$message
NULL
from scipy.optimize import minimize
def fn(p):
  m = p[0]
  b = p[1]
  return (1*m + 1*b - 2)**2 + (2*m + 1*b - 3)**2

start =np.r_[0,0]
minimize(fn, start,  method = 'BFGS')
  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: 8.100203955737182e-13
        x: [ 1.000e+00  1.000e+00]
      nit: 5
      jac: [ 4.056e-06  2.537e-06]
 hess_inv: [[ 9.996e-01 -1.500e+00]
            [-1.500e+00  2.500e+00]]
     nfev: 18
     njev: 6

Using root function

from scipy.optimize import root
root(lambda p: [p[0] + p[1] - 2, 2*p[0] + p[1] - 3], [0,0])
 message: The solution converged.
 success: True
  status: 1
     fun: [-2.220e-16  0.000e+00]
       x: [ 1.000e+00  1.000e+00]
    nfev: 5
    fjac: [[-4.472e-01 -8.944e-01]
           [ 8.944e-01 -4.472e-01]]
       r: [-2.236e+00 -1.342e+00  4.472e-01]
     qtf: [-7.804e-12  9.765e-13]

From the above, we see that \(m = 1\) and \(b = 1\) hence our equation is \(y = 1x + 1\) which yields the results previously obtained.

What if we have 3 data points, 100 datapoints etc? instead of + we use sum

fn2 <- function(p, X, Y){
  m <- p[1]
  b <- p[2]
  sum((X*m + b - Y)^2)
}
optim(c(0,0), fn2, X = c(1,2),Y = c(2,3), method = 'BFGS')
$par
[1] 1 1

$value
[1] 1.93566e-19

$counts
function gradient 
      14        8 

$convergence
[1] 0

$message
NULL
import numpy as np
from scipy.optimize import minimize

def fn2(p, X, Y):
  m = p[0]
  b = p[1]
  return sum((X*m + b - Y)**2)

minimize(fn2, [0,0], (np.r_[1,2],np.r_[2,3]), method = 'BFGS')
  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: 8.100203955737182e-13
        x: [ 1.000e+00  1.000e+00]
      nit: 5
      jac: [ 4.056e-06  2.537e-06]
 hess_inv: [[ 9.996e-01 -1.500e+00]
            [-1.500e+00  2.500e+00]]
     nfev: 18
     njev: 6

Note that we end up with the same results for this dataset. This was a simple dataset and a simple task. Try exercises in this section:

Exercise:

Answer Using R

  1. Note that the function pnorm is the inverse of qnorm ie pnorm(qnorm(x))=x. Now use the optimise function to obtain the inverse of dnorm(x)

  2. Using the gradient descent algorithm, find the best quadratic equation that best fits the dataset below.

    x <- 1:10
y <- c(-0.2499211,-4.6645685,-2.6280750,-2.0146818,1.5632500,0.2043376,2.9151158,  4.0967775,6.8184074,12.5449975)

  3. Using optim find a quadratic equation that best describes the dataset given in question 2 above. [2]

  4. Try out the problem at stackoverflow

  5. Try out the problem at stackoverflow

  6. beta function

Answer Using Python

  1. Note that the function scipy.stats.norm().cdf is the inverse of scipy.stats.norm.ppf ie cdf(ppf(x)) = x. Now use the scipy.optimize.minimize_scalar function to obtain the inverse of scipy.stats.norm().pdf(x)

  2. Using a gradient descent algorithm, find the best quadratic equation that best fits the dataset below

    import numpy as np
x = np.arange(10) + 1
y = np.array([-0.2499211,-4.6645685,-2.6280750,-2.0146818,1.5632500,0.2043376,2.9151158,  4.0967775,6.8184074,12.5449975])

  3. Using scipy.optimize.minimize find a quadratic equation that best describes the dataset given in question 2 above. [2]

  4. Try out the problem at stackoverflow

  5. Try out the problem at stackoverflow

  6. beta function

Back to top